TL;DR
Related Work
Introduction
이번엔 gradient-based subword tokenization module (GBST)를 만들었다. SentencePiece, WordPiece 나 raw text를 받는 token-free 모델이 아닌 training을 통해 subword representations을 학습하는 무언가다. 연구에서도 강조하는 부분이 기존 token-based 보다 성능은 유지하며 속도 개선을 했다는 포인트다.
Architecture
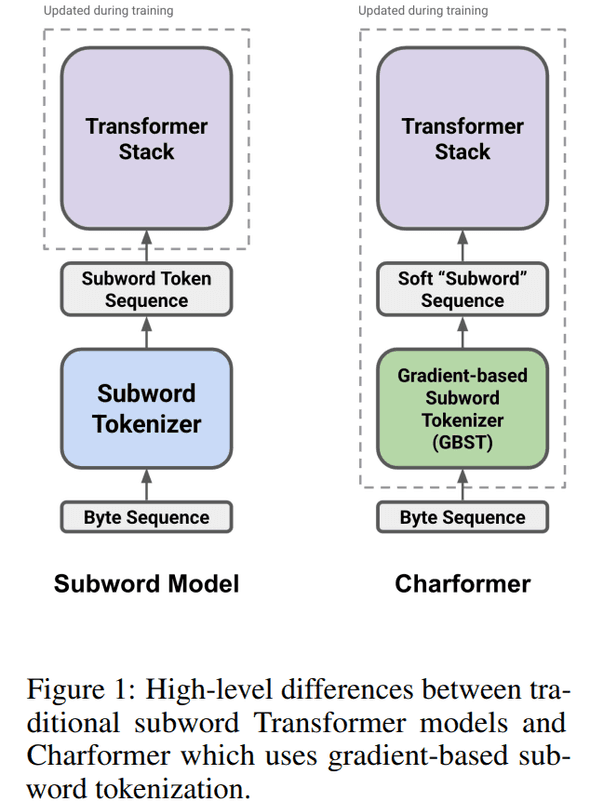
기존 pretrained token-based model 인 경우엔 왼쪽처럼 token 이 모델에 들어가고 Transformer model 만 학습하는데, CharFormer 는 tokenizer 부분까지 학습 대상입니다.
Gradient-based Subword Tokenization (GBST)
input to GBST는 , = sequence length (input characters, utf bytes), = character embedding dimension
학습을 통해서 최적의 subword segmentation을 찾는다고 한다.
a subword (block) 은 다음과 같이 정의할 수 있다.
of length for
Constructing Candidate Latent Subword Blocks
= stride, = subword blocks of size for , = maximum block size, = (non-parameterized) strided pooling function
sequence of character embedding , single subword block representation
subword blocks는 다음과 같이 표현이 가능합니다.
실제로는 stride 와 block size 를 같게 세팅해서, 다시 쓰면 요렇게 쓸 수 있습니다.
여기서 고민 포인트가 2가지 있을 수 있는데,
- strided implementation
- intra-blocks positions (ordering of characters)
strided implementation 이 어려웠던 이유가 모든 subwords 조합을 찾기가 현실적으로 어려웠기 때문에, 에 conv1d operation을 해서 smoothing 느낌을 줬다고 합니다.
subword 내 character 간 positions 정보도 중요한데, 이런 정보를 살리기 위해서 각 subword 별 positional encoding을 하려고 했지만, 이미 GBST layer에 넣기 전 conv1d를 하고 있고 mean-pooling function 를 사용하고 있어서 충분하다 판단했다고 합니다.
Block Scoring Network
모델이 어떤 block을 선택할지를 학습하기 위해서 간단하게 block scoring network 를 만들었다고 합니다. 단순한 linear transformation 형태
score는 다음과 같이 쓸 수 있습니다.
그리고 각 position 별로 (모든 block size 에 대해) 가장 적합한 block을 찾기 위해서 softmax 해서 ranking 하는데, 공식은 다음과 같습니다.
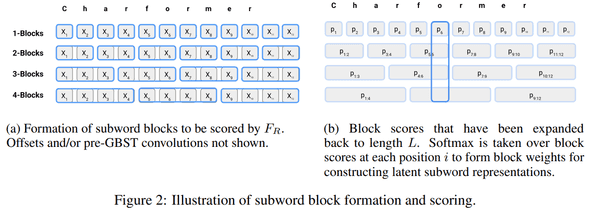
아래 이미지와 같이 동작합니다.
Forming Latent Subwords
scoring 후에는 모든 subword blocks 에 대해서 sum 합니다.
한 줄 정리하면 position 별로 optimal subword block을 학습하게 됩니다.
Position-wise Score Calibration
위와 같이 계산하면 각 position 별로 독립적인데, 각 position 별로 서로 봐주는(?) 무언가가 있으면 더 좋지 않을까라 생각해서 모든 position에 대해서 dot product 해서 score를 구하는 module을 만들었다고 합니다.
,
Downsampling
마지막으로 candidate block을 구한 후, sequence length 를 줄이기 위해서 downsampling 을 합니다.
downsampling function , sequence of latent subwords to
Transformer Stack
T5와 큰 차이점은 없고 (encoder-decoder architecture), 다만 character-level input을 사용하다 보니 ByT5처럼 architecture design 이 달라지는데, 그래서 re-scaling parameters를 했다고 한다 (구체적인 부분은 논문에...).
한 줄 요약하면 논문에서 비교 benchmark 가능하게끔 적절하게 조절했다고 한다.
Performance
Model benchmark
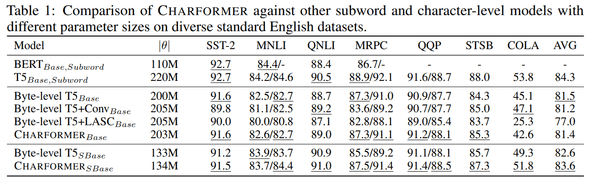
여러 모델 간 성능 비교를 했을 때 기존 T5와 comparable 한 성능을 보여주고 있다.
Speed benchmark
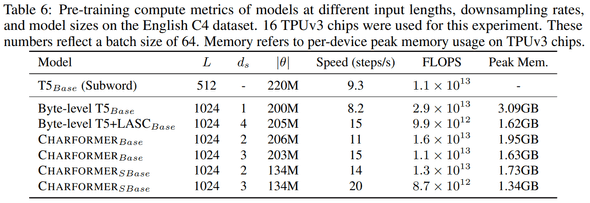
기존 character-level 보다도 학습 속도가 빠르다는 것도 보여주고 있다.
Conclusion
tokenizer를 trainable 하도록 넣은 점에서 재밌는 연구였다. 아쉬운 점은 다른 architecture (e.g. encoder-only, ...)와 task에 대한 실험이 있었으면 좋았을 거 같고 inference 도 학습 연산량, 속도 이외에 더 다양한 자료가 있으면 실제로 얼마나 차이가 있는지 더 와닿지 않았을까 생각이 들었다.
결론 : 굳굳