TL;DR

평소에 speaker diarization task 에 정말 관심이 많고, 이전에 이쪽 분야 (speech domain 쪽 전반적으로) 업무를 하다가, 최근에 다시 이쪽 분야 trend 는 어떤지 궁금해서 예전에 UIS-RNN 기반으로 speaker diarization pipeline 구현하던 게 생각나서 찾아보다 발견해서 읽게 됐습니당.

paper : arXiv

code : github

Related Work

DL approach Speaker Diarization 논문들

• UIS-RNN : paper
• BLSTM-EEND : paper
• SA-EEND : apper
• RPNSD : paper
• DNCSD : paper

Introduce

18년도에 구글에서 UIS-RNN 이란 d-vector based feature extractor speaker diarization 이 나왔는데, Sample Mean Loss (SML) 을 사용해 speaker 의 turn behavior 를 더 잘 잡는다고 합니다.

결론적으로 이번에 제안한 method 가 online method 에서 UIS-RNN 보다 성능이 올라갔고, offline method 에서 AHC (Agglomerative Hierachical Clustering) w/ PLDA scoring 과 비슷한 성능을 낸다고 캅니다.

Proposed Approach

embeddings $X = (x_1, ..., x_T)$, speaker labels $Y = (y_1, ... y_T)$ (T는 no of frames) 이라고 할 때, diarization task 를 확률 모델 적으로 아래 식으로 joint probability 를 maximize 할 수 있죠

$\hat{Y} = arg max_{Y} P(X, Y)$

이 문제를 online generative problem 으로 바꿔본다면, 식이 아래와 같이 써 볼 수 있겠죠?

$p(x_t, y_t, z_t\|x_{[t-1]}, y_{[t-1]} z_{[t-1]}) = p(x_t\|x_{[t-1]}, y_t) * p(y_t\|y_{[t-1]}, z_t)) * p(z_t\|z_{[t-1]})), (time t)$

$x_t, y_t, z_t$ 에 대한 조건부 확률을 순서대로 보면

• $x_t$ : sequence generation
• $y_t$ : assignment (speaker)
• $z_t$ : speaker change

UIS-RNN 에서...

• speaker change 는 coin flipping process 로 $p_0$ 란 transition parameter 1개로 처리 되었고
• speaker assignment 는 distance dependent Chinese Restaurant Process (ddCRP) 로 bayesian non-parametric process 로 풀었고 (time domain 에서 얼마나 화자가 교차로 배치되었는지?)
• sequence generation 은 GRU (Gated Recurrent Unit) 을 사용해서 처리

UIS-RNN

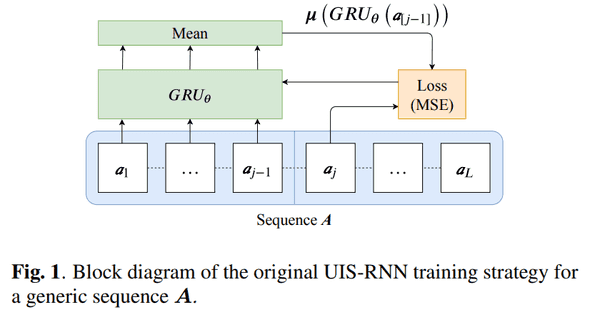
기존의 UIS-RNN은 아래와 같은 diagram 처럼 훈련이 되고 있는데요,

Dataset $D = {(X_1, ..., X_M), (Y_1, ..., Y_M)}$ ($M$, sequences of embeddings, related labels) 이라 하면, $\theta^*$ 를 통해 아래와 같은 log likelihood 를 minimizing 시키는 겁니다.

$L = \sum_{m=1}^{D} - ln p(X_m\|Y_M;\theta)$

위에 sequence generation 에 대한 formula 와 바로 위 log likelihood 식을 MSE fashion 으로 적어보면 다음과 같습니다.

$L_{MSE} = \sum_{i=1}^{\|D_A\|} \sum_{j=1}^{\|A_i\|} \|\|a_{i,j} - \mu (GRU_{\theta} (a_{i, [j-1]}))\|\|^2$

또, data augmentation 을 진행하는데, S 명의 화자, P permutations 가 적용된다면, $D_A = (A_1, ..., A_{S \times P})$, each sequence 인 $A_i = (a_{i,1}, ..., a_{i,L_i} \in D_A$ 들은 concat 되고 random 하게 permute 됩니다.

그런데 여기서 sequences 가 shuffle 된다면, 다음에 어떤 embedding 이 와야하는 지, observation 간의 어떠한 관계를 학습을 못하게 되죠. 위 공식과 같이 네트워크는 각 embedding 들의 mean distribution 을 예측하도록 학습되겠죠!

UIS-RNN-SML

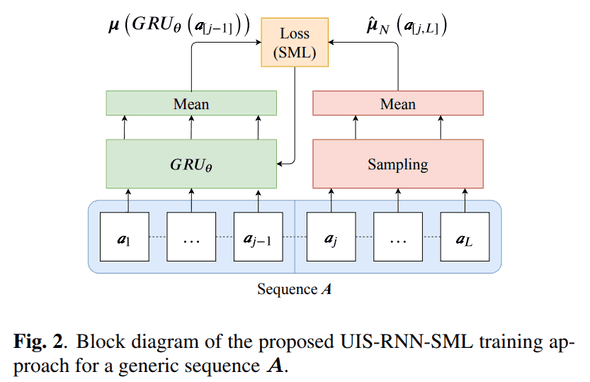
이번 논문에서 제안한UIS-RNN-SML은 아래와 같은 diagram 처럼 훈련이 되고 있는데요,

이전 UIS-RNN 과 비슷하지만, $1 ~ j-1 th$ embeddings 와 $j ~ L th$ embeddings 부분을 sampling 해서 똑같이 mean 해서 구한 후 MSE 를 구해줍니다.

이렇게 $j - 1 th$ 이후의 sequence 를 sampling 해서 mean 해서 구한다고 해서 네이밍을 Sample Mean Loss 라고 했군요.

그럼 공식은 조금 변형되서 이렇게 되겠네요

$L_{MSE} = \sum_{i=1}^{\|D_A\|} \sum_{j=1}^{\|A_i\|} \|\|E(s(i)) - \mu (GRU_{\theta} (a_{i, [j-1]}))\|\|^2$, $s(i)$ = embedding distribution of i-th speaker

하지만 실제 probability distribution 은 없기도 하고 제한된 레이블된 데이터로 하다보면 overfit 될 거 같은 느낌이 들 거 같다면서, unseen samples 에 대한 mean 을 예측하는 network 를 위해 gt 를 만들었다고 하네요.

permuted sequence 에서 직접 랜덤하게 가져왔다는데, generic sequence $A_i$ 에 대한 subset $H = (h_1, ..., h_N)$, $N$ 은 랜덤하게 sample 된 embedding, 즉, $\hat{\mu_A} (A_i) = (\sum_{i}^{N} h_i) / N$ 로 써 볼 수 있겠네요. ($N$ 이 아니라 $N - i$ 아닌가)

그럼 식을 다시 써 보면 이렇게 되겠네요.

$L_{SML} = \sum_{i=1}^{\|D_A\|} \sum_{j=1}^{\|A_i\|} \|\|\hat{\mu_A}(a_{i,[j,L_i}) - \mu (GRU_{\theta} (a_{i, [j-1]}))\|\|^2$

New Speaker Probability

이전에 UIS-RNN 의 큰 장점 중 하나가 unbounded 된 화자 수를 모델링 했다는 점인데 (ddCRP), 이전에 보였던 화자와 새롭게 등장한 화자로 switching 이 잘 된다는 점 입니다.

아래처럼 써 볼 수 있을텐데,

$p(y_t = k\|z_t = 1, y_{[t-1]}) \propto N_{k,t-1}$

$p(y_t = max(y_{[t-1}) + 1\|z_t = 1, y_{[t-1]}) \propto \alpha$

$N_{k,t-1}$ 은 speaker $k$ 에 대한 연속적인 segment 들. 여기서는 $\alpha$ 란 parameter 하나에 의해 결정됩니다. 만약 $\alpha$ 가 크다면 speaker 수를 과대평가(?) 할 수도 있겠죠.

그래서 이 부분을 다시 제안하는데,

$\alpha = \frac{\sum_{m=1}^{D} (max(Y_m) - 1)}{\sum_{m=1}^{D} \sum_{t=1}^{Y_m} 1 (y_{m,t} \ne y_{m,t+1})}$

이렇게 하면 잘못된 metric 이나 휴리스틱하게 결정되는 거로부터 방지가 가능하겠죠

Experiment Result

DIHARD-2 Benchmark

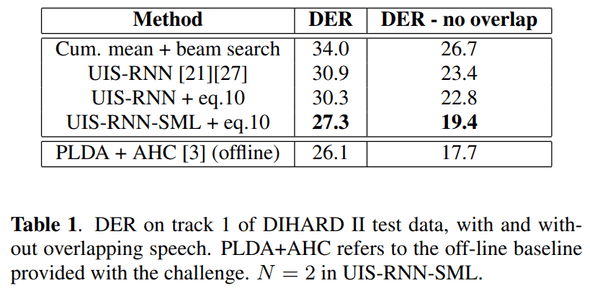
해당 dataset 에서 evaluate 했을 때, UIS-RNN 보다 outperform 한 성능을 보여주네요.

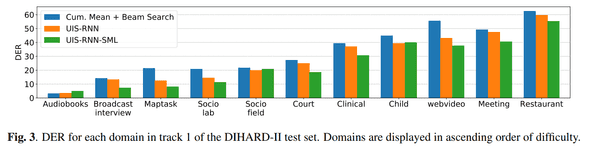
각 환경에 따른 DER (Diarization Error Rate) 변화도 보여줬는데, Audiobooks 이외엔 전부 outperform 합니다.

이 부분을 논문에서도 설명하는데, UIS-RNN-SML 은 평균을 더 잘 맞추려 하고, cluster 간 variance 가 작다는 점에서 대부분의 cases 에선 잘 동작하는데, 화자 수가 거의 없는 환경에서는 performance degradation 이 존재할거라 합니다 (by $\alpha$, $p_0$).

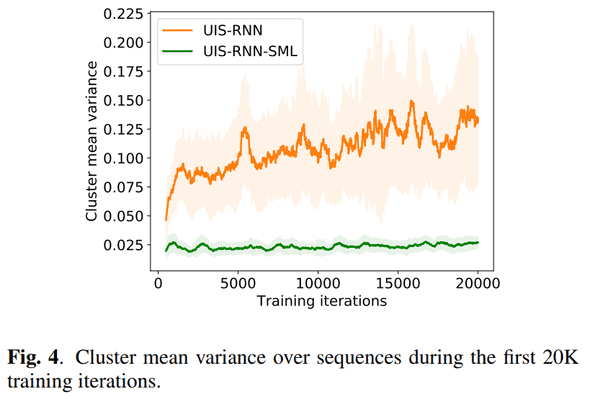
Cluster Mean Variance (at training time)

SML 적용으로 cluster 간 variance 가 stable 해진 점도 굳

Conclusion

UIS-RNN 같은 경우엔 d-vector 을 feature extractor 로 사용하는데 v1 ~ v3 까지 dataset 과 training recipe 차이에 따라 엄청난 성능 비약이 있어서, 요걸 실제로 재현하거나 훈련할 수가 없었습니다.

이전에 직접 훈련한 feature extractor 기반으로 했는데 좋은 성능을 기대하진 못했습니다 ㅠㅠ

물론 아직도 더 많은 종류의 dataset, 더 좋은 training recipe 에 따라 (feature extractor 의 성능) speaker diarization 성능이 어쩌면 (당연하게?) 결정된다고 생각하는데, 더 많은 dataset 과 pre-trained 모델이 공개되면 좋겠다란 바람이 있네요!

그래도 해당 논문은 x-vector 기반으로 재현을 하였고, SML loss 사용이 전 make sense 하고 좋은 method 라 생각해서 재밌게 읽었습니다!

특히 cluster 별 mean variance 가 거의 일정하게 낮음을 유지하는 부분이 인상적 이였고, speaker embedding 을 extract 할 때 x-vector 가 아닌 구글이 가지고 있는 d-vector v3 을 사용했으면 얼마나 더 좋은 성능이 나왔을 지도 궁금해 지네요.

결론 : 굳굳